Инструментальный потенциал метода Ходрика−Прескотта на примере оценки радиогенной заболеваемости раком предстательной железы для персонала предприятия
Инструментальный потенциал метода Ходрика−Прескотта на примере оценки радиогенной заболеваемости раком предстательной железы для персонала предприятия
Аннотация
На примере оценки избыточного (радиогенного) рака предстательной железы в когорте ПО «Маяк» показано, что типично принимаемая гипотеза о приблизительно пропорциональном дозо-зависимом приросте годовых показателей риска для всех возрастных групп персонала по отношению к спонтанной заболеваемости для этой локализации онкологических заболеваний может существенным образом нарушаться. По этой причине типовые методы максимального правдоподобия и методы стандартизации показателей по возрасту, являющиеся развитием концепции пропорционального риска (линейных, экспоненциальных и пр.), не гарантируют получения адекватного результата исследования неоднородных когорт. В качестве альтернативного инструмента предлагается способ разведочно-дескриптивной оценки динамики годового показателя онкологической заболеваемости в условно-однородных выборках, являющийся развитием метода Каплана-Майера с применением приёмов статистической фильтрации. Способ не позволяет полностью заменить собой правдоподобные методы косвенной оценки показателей риска и силы связи «доза – эффект», однако он будет полезен при уточнении математических моделей и при корректном выборе функционала максимального правдоподобия эпидемиологами-статистиками.
1. Введение
Оценка интенсивности заболеваемости или смертности является важнейшим практическим инструментом изучения состояния здоровья населения. Динамика численных значений этих показателей, собственно, и указывает на состояние общественного здоровья. Заметим, что интерес представляют не столько общая смертность, сколько анализ специфических показателей смертности от отдельных причин или специфической интенсивности заболеваемости в связи с конкретным заболеванием. Их статистические приёмы оценки учёные начали разрабатывать ещё задолго до трансформации статистики в отдельную науку . К сожалению, до сих пор не найдено надёжных количественных показателей индивидуального типа. Об этом можно легко сделать вывод по достигаемой типичной точности постановки индивидуальных диагнозов, которая по утверждению дипломированных врачей-профессионалов обычно не превышает ~66% даже при использовании специализированных тестов, учитывающих несколько признаков (факторов). Поэтому дальше в статье речь пойдет только о фактически применяемых групповых или даже массовых статистических показателях, что предполагает их одинаковое понимание и применение специалистами здравоохранения и работниками федеральной службы государственной статистики.
Наибольший интерес в изучении показателей смертности или заболеваемости связан с их возможной зависимостью от разнообразных факторов риска и их сочетаний. Наиболее очевидные из них — возраст и пол; менее очевидные — образ жизни, диета, неблагоприятная экологическая обстановка, принадлежность к профессиональной группе. По указанным причинам показатели обычно имеют значительную вариабельность между различными подгруппами населения, поэтому их оценка – это всегда оценка в конечной выборке, подверженной влиянию случайной неопределенности наблюдений. Например, это могут быть какие-то региональные группы, профессиональные коллективы работников, пациенты госпиталей и т.п. — для всех показатели будут различаться. Однако исследователь заинтересован в получении оценок, устойчивых к случайным возмущениям, как если бы он работал с генеральной совокупностью однородных данных.
Традиционно, стабилизация оценок может достигаться путем усреднения показателей по стратифицированным подгруппам выборки. При этом ввиду сильной зависимости динамики от возраста, в первую очередь осуществляется стратификация именно по возрастным группам, на чем основывается так называемое «определение» показателя в качестве дроби от деления числа изучаемых специфических событий M (за период наблюдения) на число прожитых человеко-лет A в исследуемой страте за этот же период , , т.е. . Однако этот вычислительный приём обладает недостатками, свойственными своему математическому смыслу — ведь мы получаем ничто иное, как разностную производную от недифференцируемой функции. Очевидно, во-первых, что стратификация по возрасту ухудшает временнóе разрешение метода. Во-вторых, происходит не вполне однозначное переопределение одной неизвестной величины h через другую неизвестную величину A, поскольку часто оказывается, что разные исследователи понимают последнюю по-разному. В-третьих, стохастическая природа отсчётов «случаев» M никуда не пропадает, но только лишь происходит уменьшение неопределенности оценок при увеличении
Это в принципе не позволяет работать с малым числом специфических наблюдений M. По такой причине все эпидемиологические и социо-демографические исследования заболеваемости или смертности — это всегда крупномасштабно, в то время как результаты хотелось бы получать и для коротких периодов наблюдения, и в малых почти однородных группах. Хотя бы в масштабе предприятия или небольшого района. Наконец, в-четвёртых — использование категории «человеко-годы» подталкивает исследователя к совершению ошибок в процессе стратификации исследуемой выборки, если внутри неё одновременно действует несколько факторов риска. Это приводит к ложному толкованию величины h как показателя событий — вместо правильного понимания функции h(t) как процесса, развивающегося по мере старения когорты .
Целью предлагаемой статьи является демонстрация новой методики мониторинга динамики групповых интенсивностей заболеваемости или смертности в выделенных когортах сравнительно небольшого размера (до нескольких тысяч человек), исключающей влияние маскирующего усреднения по возрасту и использования ненаучной категории «человеко-лет наблюдения», но опирающейся на понятие случайного процесса.
Действительно, если заглянуть в историю возникновения понятия показателей на примере первых таблиц смертности Граунта и Галлея (таблицы дожития, они же – порядковые статистики) , , можно заметить, что понятие «человеко-годы» изначально не применялось, но показатели интенсивности смертности в таблицах Галлея, тем не менее, рассчитывались. То же самое справедливо и в отношении первичной заболеваемости. Длительное время этот метод не получал широкого распространения в силу больших вычислительных затрат (при ручном счёте). В середине прошлого века он был обобщён и для изучения специфических заболеваемости и смертности — тоже без использования категории человеко-лет наблюдения. Дескриптивные характеристики этого метода известны сейчас под названиями показателей Каплана–Майера (KM) и Нельсона–Аалена , . Главное их преимущество — отсутствие необходимости проводить стратификацию наблюдений по возрасту вместе с отсутствием необходимости искусственно задавать границы страт. Более того, возможен учёт влияния на статистику каждого специфического «случая», т.е. можно сохранить естественное для наблюдений разрешение во времени. Недостаток в том, что показатели Каплана – Майера и Нельсона – Аалена кумулятивные и условные в том смысле, что связаны с выбытием изучаемых лиц из-под наблюдения только вследствие дожития до специфического события и как если бы изучаемые заболеваемость или смертность были единственными причинами выбытия. Иными словами, они не являются истинными вероятностными показателями. Однако этот недостаток может быть обращен в преимущество, позволяя находить процесс изменения показателя h(t) как простую операцию математического дифференцирования, поскольку специфическая заболеваемость или смертность тоже относятся только к тем лицам, которые дожили до рассматриваемых событий. Только дифференцировать нужно не эмпирические (недифференцируемые) оценки, а некую сглаженную аппроксимацию, отфильтрованную от стохастической составляющей ради достижения бóльшей устойчивости.
Широкое распространение высокопроизводительной и доступной вычислительной техники полностью решает проблему трудоёмкости вычислений. Благодаря этому численные методы фильтрации наблюдений далеко не редкость. Например, к использованию может быть рекомендован известный метод Ходрика−Прескотта , который однажды уже применялся для фильтрации рядов эпидемиологических наблюдений , если не требуется использование метода для целей прогнозирования ещё не наступившего будущего. Строго говоря, в более продвинутой форме он предлагался ещё в СССР задолго до публикации вышеназванных авторов, а также он известен как метод регуляризации Тихонова .
2. Материал и методы
2.1. Описание метода
В основе лежит корректное вероятностное определение интенсивности специфических событий , которое можно выразить формулой , где
— условная вероятность «здорового» дожития в том же смысле, как это указано выше. Полезно отметить ещё две формы записи данного определения, тесно связанные с его смыслом:
Одна из формул отражает тот очевидный факт, что дескриптивная ожидаемая выборочная скорость процесса выбытия индивидуумов из-под наблюдения прямо пропорциональна ожидаемой численности оставшейся выборки. Тогда h(t) — дескриптивный «скользящий» коэффициент пропорциональности, зависящий от возраста наблюдения. Другая формула прямо указывает, что условная вероятность , может быть вычислена только при рассмотрении всех последовательных шагов процесса выбытия в выборке. При этом, если до момента времени t0 ни одного случая заболевания не наблюдалось, можно положить
что позволяет оперировать понятием «кумулятивный риск»:
, где
— кумулятивная интенсивность процесса. Отдельными исследователями величина
также может именоваться в качестве кумулятивного риска , поскольку в случае анализа редких событий величины R и H могут различаться не более, чем на 1‰ вплоть до
Заметно бóльшие различия характерны только для госпитальных выборок или при анализе болезней системы кровообращения в популяционных группах.
Это — хорошо известные , , формулы, которые могут быть полезны не только в теории. Эмпирическими интегрально-разностными аналогами величин и
являются показатели Каплана–Майера и Нельсона–Аалена, которые введены специально для целей исследования специфических показателей смертности или заболеваемости. То есть они являются непосредственным развитием фундаментальной работы Галлея, который ограничивался только анализом общей смертности. Для наших целей будем применять только один из них, поскольку связь (1) между показателями уже известна.
Согласно методу Каплана-Майера, в процессе длительного наблюдения за выборкой объема NΣ удобно выбрать в качестве временнóй (возрастной) сетки фиксации отсчётов ti моменты наступления изучаемых специфических событий. Если выборка не является очень большой, то общее число событий MΣ может быть невелико настолько, что для каждого полуоткрытого интервала времени (ti-1, ti] в момент ti возможна фиксация редких или даже единичных случаев Mi на фоне Ni-1 количества лиц, доживших до попадания в соответствующий временной интервал (ti-1, ti]. Тогда интервальная апостериорная оценка вероятности pi условно здорового дожития без наступления специфического события вычисляется элементарно как 1-Mi/Ni-1. Соответственно, становятся доступными апостериорные точечные оценки временного ряда функции условно здорового дожития — значения показателя Каплана-Майера:
При этом обычно ещё до наблюдения самого первого «случая» начало периода наблюдения t0 тоже естественно включить в состав временного ряда с числовым значением показателя KM0≡1, поскольку это вполне информативная точка. От показателя (2), являющегося эмпирическим аналогом условной вероятности здорового дожития, опираясь на (1), можно перейти к фактически эмпирическому временному ряду кумулятивной интенсивности заболеваемости/смертности
для которой приращения отсчётов являются независимыми случайными величинами. Именно этот временной ряд нуждается в фильтрации, то есть замене некоторым другим статистически незначимо отличающимся от Hk, но регулярным временным рядом Fk, по которому возможно аналитическое восстановление всей зависимости h(t) вместе с hk=h(tk).
Будем использовать методы опирающиеся на минимизацию функционала информационных потерь, в котором штрафуются как отклонения Hk-Fk, так и слишком нестабильное поведение величины производной, заведомо принадлежащей к некоторому классу регулярных функций. По смыслу рассматриваемой нами задачи в состав штрафной функции целесообразно включить вторую производную показателя интенсивности h''(t) при условии аппроксимации кумулятивной интенсивности Hk кусочно-кубическими сплайнами F(t), непрерывными вместе со своими первыми и вторыми производными. В такой постановке эволюционную задачу оценки h(t) формально удаётся свести к краевой задаче со смешанными граничными условиями в начальной t0 и конечной tn точках на оси возраста. Техника вычислений во многом аналогична работе . Функционал оценки имеет вид:
где F и m — векторы взаимосвязанных параметров кусочно-кубических сплайнов, определённые на сетке узлов, как Fk=F(tk) и mk=h'(tk); reg – это неотрицательный параметр регуляризации. Минимизация функционала (4) должна производиться с учётом непрерывности показателя интенсивности процесса в точках «сшивки» решения h(tk-0)=h(tk+0). Это приводит к соотношению B⋅m=A⋅F, где некоторые матрицы A и B зависят от сложившегося характера расположения узлов отсчёта tk, причём матрица B квадратная, симметричная, положительно-определенная и трёх-диагональная. Более того, можно показать, что интеграл в функционале (4) может быть точно представлен в виде скалярного произведения , благодаря чему он строго квадратичен по параметрам и всегда имеет единственный минимум
где E — единичная матрица. При выборе нулевого параметра регуляризации никакой фильтрации не происходит, и решение задачи превращается в интерполяцию, практического смысла в которой нет из-за преобладания стохастических помех. Небольшое положительное значение reg выбирается адаптивно так, чтобы со статистической точки зрения решение Freg отличалось бы от эмпирического вектора H незначимо, и исследователь риска мог бы обоснованно считать компоненты вектора Freg почти истинными значениями кумулятивной интенсивности процесса. Для этой цели в качестве средства контроля подходит числовая оценка девиации биномиального функционала правдоподобия для всех шагов исследуемого процесса в совокупности с учетом независимости приращения отсчётов, если девиацию отсчитывать от точки насыщения (от точки интерполяции):
Как известно , остаточная девиация ведет себя приблизительно как величина хи-квадрат с n-1 степенью свободы, поэтому её отклонение от нуля на уровне может служить хорошим ориентиром, достаточным для выбора параметра reg. Практика вычислений показывает, что вполне достаточно даже попадания в центр распределения хи-квадрат, т.е. достижение уровня
2.2. Описание эмпирического материала
В качестве объекта исследования интенсивности заболеваемости была изучена представительная выборка работников ПО «Маяк» , , , , сформированная практически из всех работников-мужчин предприятия за период наблюдения более 60 лет. Изучаемый эффект — рак предстательной железы (РПЖ; С61 по коду МКБ-10) – одно из наиболее распространённых злокачественных новообразований у мужчин. Цель исследования заключалась в попытке понять, существует ли связь между повышенной заболеваемостью РПЖ и профессиональной деятельностью, связанной с возможным хроническим воздействием ионизирующей радиации на рабочих местах, что присуще профилю работы предприятия. Несмотря на то, что свойство радиационно-онкологического влияния ионизирующего излучения, казалось бы, хорошо изучено, в отношение РПЖ убедительных доказательств не было получено как для когорты ПО «Маяк» , , , так и для объединенных когорт профессиональных работников ядерных производств США и Англии . В то же время ряд прямых исследований и косвенных наблюдений позволяет считать, что вопрос об актуальности продолжения исследования не может быть снят с повестки.
Здесь уместно отметить, что авторы большинства работ по влиянию ионизирующего излучения на РПЖ , , , , прекрасно понимали всю ограниченность инструментальной точности применения традиционных методов стратификации наблюдений и таблиц дожития. По этой причине поиски связи избыточной заболеваемости с воздействием радиации производились либо с применением методов стандартизации показателей (т.е. кумулятивно), что чревато влиянием эффекта усреднения и потерей информации, либо выполнялись с помощью методов максимального правдоподобия на основе так называемых «моделей», то есть в значительной мере почти вслепую.
Предлагаемый нами метод выгодно отличается тем, что результат исследования можно оценивать даже визуально хотя бы для некоторых условно однородных групп, т.е. в его основе лежат не непроверенные гипотезы, а практически сами эмпирические данные, отфильтрованные от случайных отклонений.
В качестве исходного материала в анализе использован регистр персонала ФГУП ПО «Маяк», содержащий индивидуальные данные об уровнях радиационного воздействия и описание нерадиационных факторов риска для работников трех заводов основного производства и ряда вспомогательных производств . Общая численность по состоянию на 31.12.2013 составила 19 395 мужчин. Женский персонал в анализ риска заболеваемости раком предстательной железы (РПЖ) не включался по естественным причинам. Рассмотренный регистр мало отличается от своего прототипа, рассмотренного в работе , где анализировалась заболеваемость среди работников трех основных заводов ПО «Маяк». Для них сбор дозиметрической информации производился наиболее полно благодаря почти поголовному индивидуальному дозиметрическому контролю.
Начало наблюдения определялось датой найма на ПО «Маяк». Средний возраст найма составил около 23 лет. Средняя продолжительность жизни на дату 31.12.2013 – 59,6 лет. К указанной дате умерло 13 668 мужчин (70,6% списочного состава регистра). Средняя реконструированная эквивалентная доза облучения на стенку мочевого пузыря составила 422,5 мЗв. Использованы коэффициенты эквивалентности для внешнего проникающего излучения и
для внутреннего облучения инкорпорированным плутонием. Значения доз определялись кумулятивно на конец жизни или к моменту постановки диагноза РПЖ, в зависимости от того, какое событие означало фактическое прекращение наблюдения. Всего сколько-нибудь значительному воздействию ионизирующего излучения с кумулятивными зарегистрированными дозами более некого условного фонового предела в 50 мЗв за время наблюдения подвергалось 13875 работников мужского пола. Остальные имели дозы до 50 мЗв либо не состояли на индивидуальном дозиметрическом контроле и не направлялись на биофизическое обследование на носительство соединений плутония. В среднем в расчете на стенку мочевого пузыря у персонала преобладало внешнее облучение — кумулятивную поглощенную дозу гамма-излучения более 50 мГр получило 13845 человек; кумулятивную дозу внутреннего альфа-облучения более 2,5 мГр получило 455 человек. Таким образом, статистическая возможность связать заболеваемость РПЖ с внутренним облучением представляется весьма призрачной, даже если такая связь объективно существует. Ионизирующее воздействие измерено и реконструировано в соответствии с дозиметрической системой MWDS-2013 , принятой для производственного объединения «Маяк» в Южно-Уральском институте биофизики ФМБА.
3. Результаты применения метода и обсуждение
Радиогенная заболеваемость статистически может быть определена только в виде избыточной заболеваемости при сравнении групп работников с различной лучевой нагрузкой. Такой подход к оценке объясняется морфологической неразличимостью спонтанных и радиогенных РПЖ. Наиболее просто провести сравнение двух групп: со сравнительно высокими и c почти фоновыми дозиметрическими показаниями, в остальном полагая эти группы практически однородными. Результаты наблюдений кумулятивного показателя интенсивности заболеваемости до применения фильтрации и после применения приведены на рисунке 1. Регуляризованная оценка годового показателя — на рис. 2.
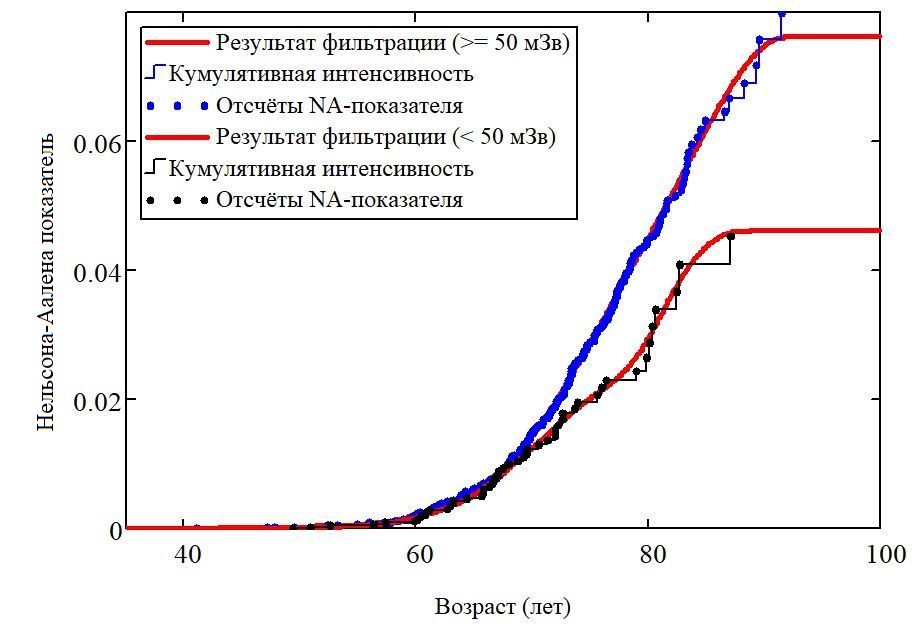
Рисунок 1 - Сопоставление кумулятивных зависимостей интенсивности заболеваемости РПЖ в разных дозовых группах, разделенных по условной границе 50 мЗв на стенку мочевого пузыря от внешнего гамма-излучения за всю жизнь
Примечание: эмпирические данные получены как непараметрические оценки показателя Нельсона-Аалена
Таблица 1 - Разведочная оценка связи событий заболевания РПЖ с дозой ионизирующей радиации
Дозы, мЗв (γ; средняя и диапазон) | Случаи РПЖ | База исследования | |
Облученная группа | 578,66 (50,01 … 7310,29) | 248 | 13845 |
Группа сравнения | 15,24 (0 … 49,99) | 50 | 5550 |
Итого | — | 298 | 19395 |
Примечание: оценка относительного риска статистически значима на уровне значимости p<0,001 по Пирсону. Оценки доверительных интервалов относительного риска даны по Zou – Donner [25]: RR=1,99(95%CI:1,47 ... 2,69)
Проведенная грубая стратификация данных не вызывает сомнений в существовании статистически значимой связи между повышенной заболеваемостью РПЖ и профессиональным облучением персонала. С другой стороны, при столь грубой стратификации невозможно чётко идентифицировать характер дозовой зависимости радиогенного эффекта. Можно только предположить, что связь между кумулятивными показателями и дозой вполне может оказаться близкой к линейной. В этом случае из таблицы 1 нетрудно получить оценку на единицу дозы гамма-излучения в изученной области, в предположении, что на персонал не действовали другие незарегистрированные факторы риска, коррелированные во времени с показаниями дозиметров. Остаётся только удивляться, почему в других исследованиях , , , , столь сильная радиочувствительность и почти очевидная связь не была обнаружена.
Отчасти объяснить несовершенство оценок из работ , , , , можно по рис. 2. Нетрудно видеть, что обе возрастные зависимости имеют характерный профиль, в корне отличающийся от гипотез о поведении показателей спонтанного (фонового) и повышенного риска, заложенных в основу применения методов максимального правдоподобия в публикациях , , . В частности, традиционно, в анализе риска предполагают, что годовой показатель риска (интенсивность; “hazard”) для всех видов рака только растет с увеличением возраста в соответствии с трендом Армитажа . По факту же (рис. 2), по крайней мере, для рака предстательной железы в диапазоне возрастов 80–90+ лет наблюдается его резкое падение до нуля, несмотря на то, что к этому моменту ещё не вся когорта вымерла – в регистре ПО «Маяк» есть долгожители в возрасте до 102 полных лет. Благодаря этому использованные аппроксимационно-регрессионные модели в принципе не способны правильно описывать эмпирические данные в области старших возрастов в любых дозовых интервалах, что вызывало неизбежное смещение и центральных оценок, и границ доверительного интервала.
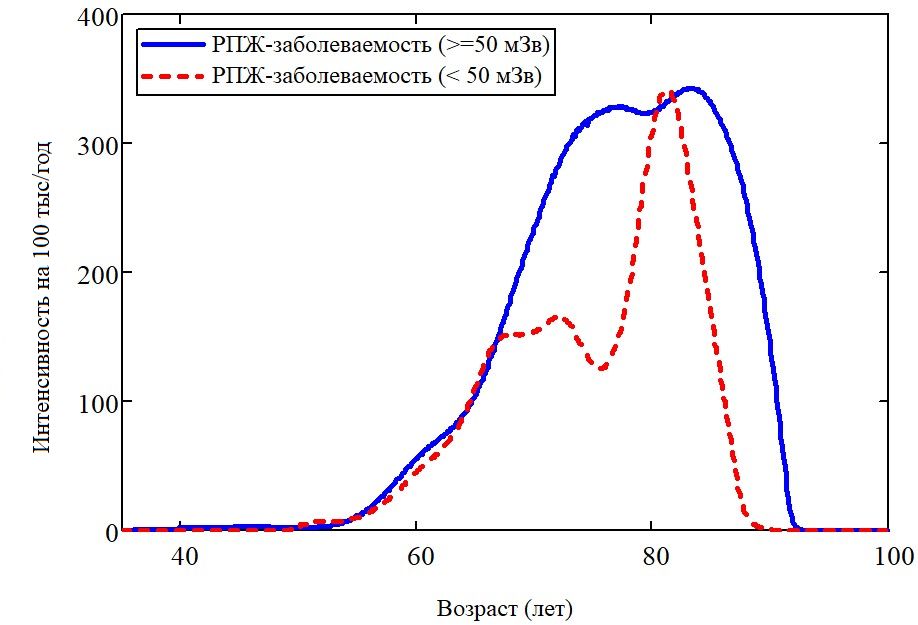
Рисунок 2 - Возрастные зависимости интенсивности заболеваемости РПЖ в двух дозовых подгруппах
Примечание: аппроксимации показателя выполнены на основе модифицированного алгоритма конечно-разностной фильтрации Ходрика–Прескотта
Нельзя пройти мимо бимодальности у зависимости h(t) в низкодозовой группе. С учётом того, что максимум первого всплеска заболеваемости приходится на возраст 70–75 лет и достигает ≈ 160 случаев на 100 тысяч человек в год среди лиц, доживших до указанного возраста, можно отождествить первый всплеск с истинной спонтанной заболеваемостью, не связанной с воздействием ионизирующей радиации. Действительно, судя по публикации , это примерно соответствует типичным значениям кумулятивной интенсивности заболевания РПЖ от 14,8 ‰ до 30,1 ‰ в Российской Федерации в период с 1997–2007 годов и средней интенсивности 266 случаев на 100 тыс. человек в год в возрастном диапазоне 70–75 лет. То есть первый всплеск — это показатель в группе условно здоровых работников. Второй всплеск отличается от первого более узкими временными рамками развития – около 15 лет, т.е. почти вдвое короче первого основного. Очевидно, он связан с фактической неоднородностью предположительно однородной малооблучённой группы. Конкретно он сформирован 7 случаями РПЖ (7 ступенек), которые можно индивидуально проследить по регистру. Оказалось, что индивидуальные дозы внешнего облучения этих работников не превосходят 40 мЗв при стаже работы на ПО «Маяк» от 24 лет до 51 года, что само по себе вызывает вопросы к службе дозиметрии при условии, что обычно, даже в условиях нашего времени в «чистой зоне» весьма затруднительно получить менее 1–2 мЗв/год выше естественного природного фона при 6-часовом рабочем дне. А все семеро начинали трудовую деятельность ещё в период становления предприятия в 1948-1958 годах, когда лучевые нагрузки были сравнительно высоки. Более того, трое из семи в разное время трудились на радиохимическом заводе. Кроме радиации, они могли быть подвержены дополнительным химическим факторам риска, а регистрации РПЖ у одного из семи работников за 13 лет до этого события предшествовало другое онкологическое заболевание — лимфосаркома. Таким образом, второй всплеск, скорее всего, обусловлен скрытыми в регистре профессиональными факторами риска, то есть указанные семь профессиональных «случаев» следовало бы отнести в другую страту. Но этот же факт означает, что на рис. 2 видна зависимость годового показателя от истории воздействия профессиональных факторов. Это означает, что для более корректной оценки силы связи «доза – эффект» методами максимального правдоподобия следует использовать динамические модели формирования показателя риска “hazard” вместо типично применяемых дескриптивных явно заданных статических моделей. Динамика формирования показателя риска заболеваемости должна иметь какое-то другое объяснение. Например, с биологической точки зрения, очевидно, что мгновенный групповой показатель риска “hazard” при описании онкологического заболевания не может безынерционно реагировать на кумулятивную дозу ионизирующего излучения.
Оценка медицинских последствий профессионального облучения среди персонала ПО «Маяк» позволяет с уверенностью говорить о наличии дозо-зависимого избыточного радиогенного риска РПЖ. В предшествующих исследованиях этот тренд не удавалось уверенно зафиксировать статистико-эпидемиологическими методами наблюдения только благодаря неочевидным ошибкам применения известных статистических алгоритмов, формалистическому подходу к описанию спонтанных рисков и очень специфическим особенностям процесса развития этого вида рака, возможно связанным с его гормонально-зависимой природой. Ранее выполненные исследования не оправдали себя практикой селекции гипотез за счёт применения теста отношения максимальных правдоподобий без проверки качества аппроксимации всей модели. Как оказалось, ошибочными также были ранее предпринятые попытки описать радиогенную составляющую интенсивности возникновения РПЖ с помощью единственного параметра избыточного относительного риска на единицу дозы (ИОР/Зв или ИОР/Гр). Если он и может применяться в отношении РПЖ, то только в том случае, если под термином «риск» понимается кумулятивная величина за определенный продолжительный промежуток времени, то есть вероятность события.
Не подтвердился вывод предыдущей работы о том, что заболеваемость раком предстательной железы в когорте работников, нанятых на основные производства ПО «Маяк» в период с 1948 по 1982 гг., была статистически значимо выше, чем показатели национальной статистики. Наоборот, показатели риска работников по максимальной годовой величине были ниже максимального общенационального уровня, то есть на предприятии наблюдался типичный «эффект здорового рабочего», однако в диапазоне возрастов 75+ из-за влияния радиационного фактора интенсивность риска достигала примерно тех же значений, что и в популяции Российской Федерации, где активно проявляют себя также некие нерадиационные факторы риска в том же самом возрастном диапазоне 75+.
Полученные результаты определенно свидетельствует о неприменимости моделей пропорционального риска или линейных моделей, по меньшей мере, к анализу годового показателя заболеваемости РПЖ “hazard”.
4. Заключение
Рак предстательной железы (РПЖ; С61 по коду МКБ-10) — одно из наиболее распространённых злокачественных новообразований у мужчин. В структуре заболеваемости раком среди мужчин России РПЖ занимает второе место после рака легкого, бронхов и трахеи (С33, С34) . На некоторых территориях, например в штате Невада (США), известном наземными и воздушными испытаниями ядерного оружия, заболеваемость РПЖ может выходить на первое место, несмотря на то, что основная часть населения на территории штата имеет совсем небольшое избыточное сопутствующее ионизирующее радиационное облучение по сравнению с естественным фоном . В таких условиях вполне закономерным является предположение о возможной существенной связи между повышенной заболеваемостью и радиацией, однако актуальной является оценка её силы.
Установлено, что в когорте персонала ПО «Маяк» присутствует статистически различимая связь между повышенными показателями риска заболеваемости раком предстательной железы и хроническим воздействием ионизирующей радиации на рабочих местах. Однако её невозможно интерпретировать в рамках популярной линейно-беспороговой теории в силу нарушения пропорционального характера отклика годовых показателей риска на кумулятивную дозу. Ясно, что поиск объяснения результата уже не должен производиться на основе явных эвристических моделей. Для разведочного анализа следует использовать методы статистической фильтрации по типу метода Ходрика–Прескотта, а для многофакторного прогнозирования групповых радиационных эффектов следует в будущем использовать динамические модели формирования показателей риска, связывая их с историей облучения на рабочих местах. Требуется создание нового инструментария оценки радиационно-эпидемиологических рисков.
Превышение годовых показателей интенсивности заболевания РПЖ над спонтанным уровнем уверенно регистрируется только в диапазоне возрастов 70+ лет. Избыточная часть общей заболеваемости запаздывает по отношению к спонтанной, что приводит к неприемлемости прогнозирования индивидуальных радиационных эффектов с помощью моделей пропорционального риска, связывающих интенсивность заболеваемости («мгновенный» показатель) и кумулятивную дозу. По крайней мере, в случае анализа заболеваемости РПЖ, кумулятивные дозы могут применяться только для предсказания кумулятивных групповых эффектов. По состоянию на конец 2013 года можно утверждать, что из 298 заболеваний РПЖ, наблюдавшихся на предприятии среди 19 395 мужчин, от 82 до 158 случаев были радиационно-обусловленными (при среднем уровне кумулятивных эквивалентных доз около 0,42 Зв). Однако в целом по когорте предприятия без учета радиационного воздействия кумулятивные показатели заболеваемости были ниже или сопоставимы со средними показателями в Российской Федерации.
Радиационный риск развития рака предстательной железы, являющегося гормонально-зависимым заболеванием, оказался также существенно зависящим от других факторов риска, идентифицировать которые рассмотренным методом по записям в регистре не удалось.
