Дискретизация данных в прогностических моделях эпидемиологии

Since the COVID-19 pandemic beginning, the demand for forecast in epidemiology greatly increased

However, this accuracy turns out to presence for a short-term prognosis (week-length), but is frequently important to know the long-term (month-length) prediction. In long-term prognosis, daily oscillations can be neglected, so just the trend is forecasted. Indeed, oscillations disturb the prognostic model and affects the result. On the other hand, there is an agent-based and cellular automata approach also used in epidemiology

To make a prognosis, we use a lag model given by a transformation (the graphical scheme of which is depicted on Figure 1):

As soon as Φ transition function is unknown, it is reasonable to determine it using a neural network as an implicit transition function. To work properly, it should be previously trained on the data available

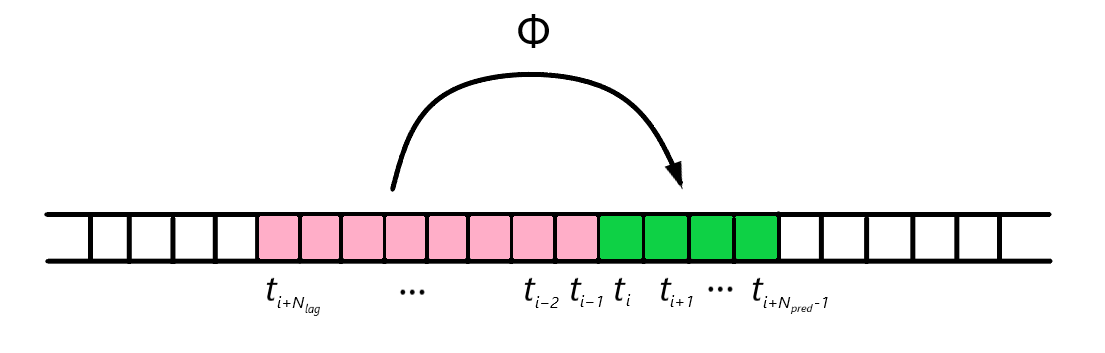
Figure 1 - Scheme of lag prediction

DOI:10.60797/BMED.2024.3.2.1

The problem arising here is that the data fed into the model for training contains noise that can affect the result. As soon as we are aimed to make a long-term forecast we may neglect it (the reproducing of the noise as accurately as the trend will require too complete model; besides, the exact noise reproduction is hardly necessary, hence it can be believed to be random on the time scales considered). One of the ways to defeat noise disturbance is smoothing

[10]

. However, instead of smoothing, our approach proposes to reduce oscillations by splitting the values range over several intervals, replacing the data value with a number of the intervals it belongs to. In other words, it can be considered as a replacing data on a temporal interval (x-axis) with the mean value on it, while the interval ends are determined from the uniform vertical slicing (see Figure 2). While selecting the value discretization intervals (y-axis), we shall mind that their length should be so that allow to remove daily oscillations, but small enough to take into account principle data behaviour features.

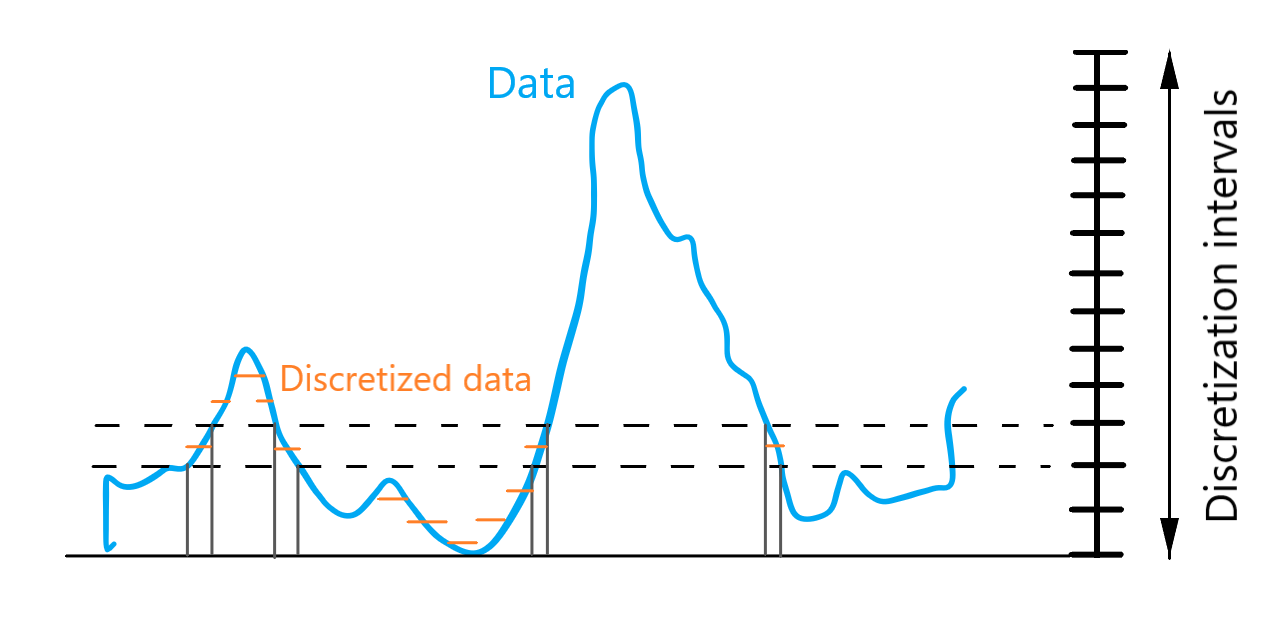
Figure 2 - Scheme of data discretization

DOI:10.60797/BMED.2024.3.2.2

Ergo, the algorithm proposed consists of the following steps:

1. to obtain a time row of a particular epidemiological indicator (as an example, number

of new recoveries over 100.000 people in Moscow);

2. to interpolate the data on a uniform grid (in fact, records may be done over irregular time interval; uniformity is required for the lag mode (see Figure 1));

3. to split the data into train and verification subsets;

4. to discretize the data over values range, as shown on Figure 2;

5. to train the model;

6. to make a prognosis on a validational range and compare with the real data on it.

As an alternative, to compare with, we will use the same scheme without discretization. Instead of point (3) in the list above, we will use EMD-smoothing

As to the model, we selected Nlag = 20 days, Npred = 10 days and neural network with 3 dense internal layers of 50 units each. The prognosis time was of 50 days. As soon as it is greater than , we made several iterations. The data values were sliced into 50 discrete intervals. For the filtered model, 2 intrinsic modes

Figures 3 and 4 demonstrates the prediction results. It is clearly seen that our (discretized) model follows the trend (Figure 4), while the filtered model loose it after 25 days, with the previous prognosis also being not very accurate (Figure 3). Surely, we may complicate and learn further the model for smoothing variant, but the discretized option already yields suitable results.

Figure 3 - Prognosis on regular data: smoothing model

DOI:10.60797/BMED.2024.3.2.3

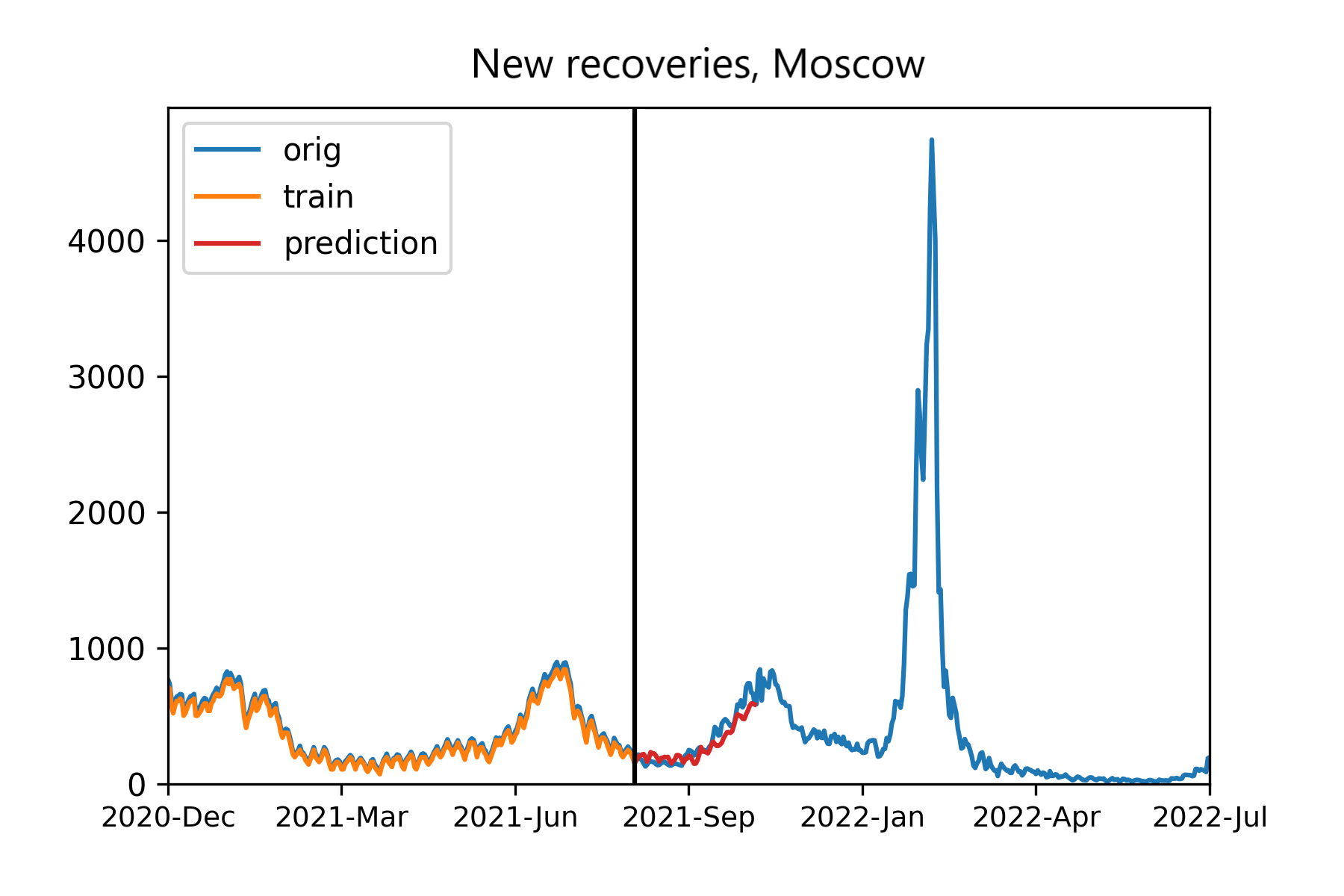
Figure 4 - Prognosis on regular data: discretization model

DOI:10.60797/BMED.2024.3.2.4

We found that the discretization allows to reach a proper result earlier than the smoothed one do; although, there is another one whilst we consider epidemiological data: the data problem. On Figure 3 one can see a sharp peak near Jan 2022. Epidemiologically, it is connected with a new virus strain appearance, but from the viewpoint of data it means the irregular behaviour. Imagine we have learnt on a previous (regular) data, but the behaviour changed, and we still need the prognosis. Obviously, it would be too presumptuously to expect from the model that it predicts the peak before it starts; however, we can start the prognosis just some time after the peak began (on a slope). The question is, will the model, trained on a regular data and on the very beginning of the peak, reproduce it properly? We may hope it, at least partially, assuming that despite the new strain appearance the principles of the disease spreading remain the same. To test it, we made two predictions, with smoothing and with data range discretization. The results are shown on Figures 5 and 6. The model with discretisation (Figure 5) does not fit the peak exactly, but it does represent at least it duration and the main form. The model with smoothing (Figure 6) fails totally, reproducing neither the duration nor the shape of the peak.

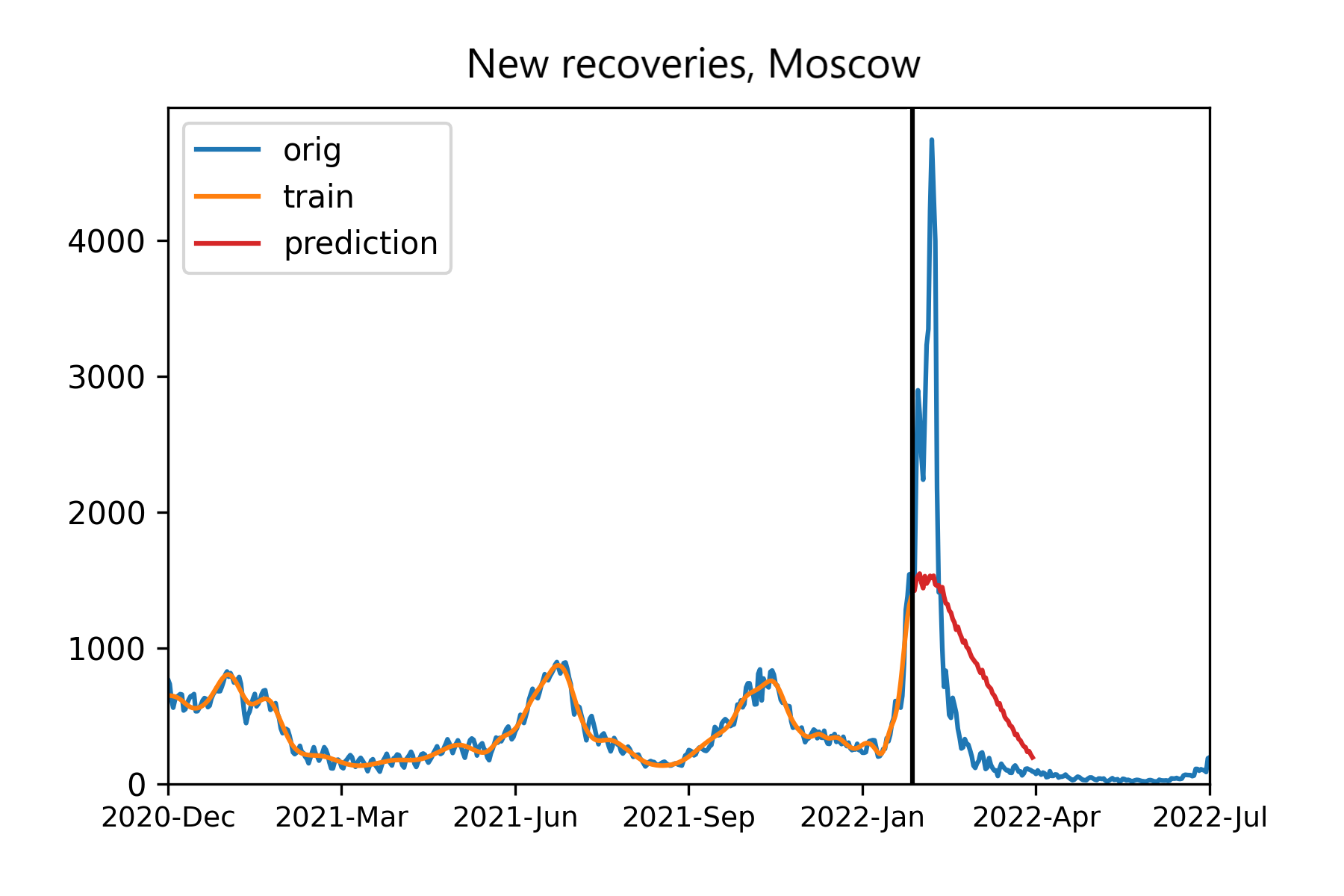
Figure 5 - Prognosis on irregular data: smoothing model

DOI:10.60797/BMED.2024.3.2.5

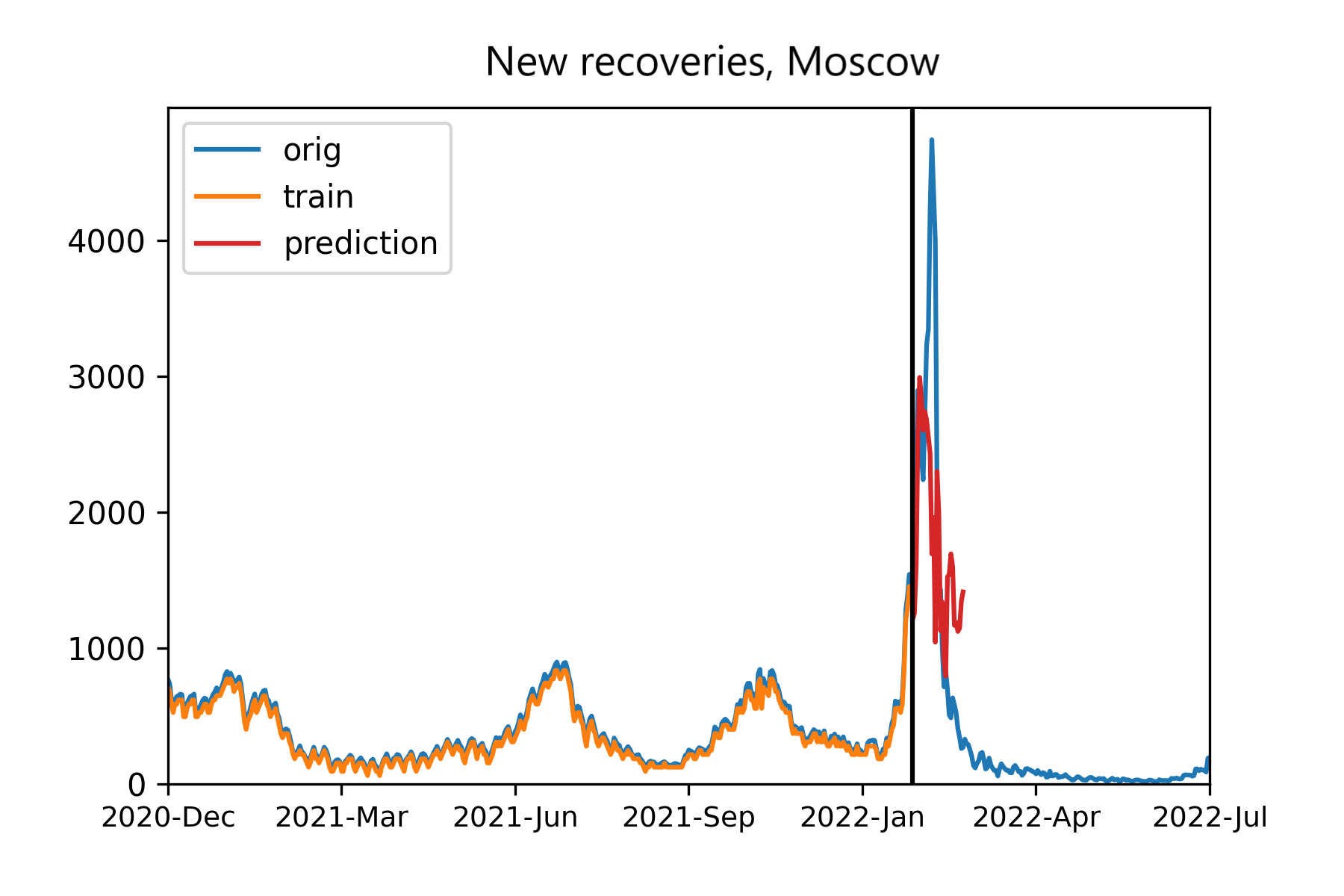
Figure 6 - Prognosis on irregular data: discretization model

DOI:10.60797/BMED.2024.3.2.6

We applied the data range discretization for the lag prediction model with neural network used for an epidemiological indicator forecast. It is shown that the approach increases the accuracy of the prognosis on the same model architecture and can be used for noise reduction instead of the smoothing. The discretization allows accurate prediction also for irregular data, which is important when the prediction required soon after the condition changed (e.g. after a new virus strain appearance). In the contrary, the same model, but with the smoothing used for noise reduction reproduce worse the regular data and makes inadequate forecast for the irregular ones. As a disadvantage, we may consider some data lack during the discretization, which disallows to use the model proposed if further differentiation may be required. Despite this for the pure prediction, for enough number of discretization intervals, it is not critical, as one can see from our forecasting results. We may recommend it as an alternative of smoothing while development forecast models. However, it should be minded that lag predictor works with a neural network, which requires enough data to be trained. These facts may limit the application of the approach proposed (for instance for common diseases like tuberculosis, whose data typically contains monthly records).