МЕДИАННАЯ БАЙЕСОВСКАЯ РЕГРЕССИЯ КАК АЛЬТЕРНАТИВА СТАНДАРТИЗАЦИИ ЭПИДЕМИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ ПРИ ИССЛЕДОВАНИИ ПРОФЕССИОНАЛЬНОГО РИСКА НА ПРЕДПРИЯТИИ
МЕДИАННАЯ БАЙЕСОВСКАЯ РЕГРЕССИЯ КАК АЛЬТЕРНАТИВА СТАНДАРТИЗАЦИИ ЭПИДЕМИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ ПРИ ИССЛЕДОВАНИИ ПРОФЕССИОНАЛЬНОГО РИСКА НА ПРЕДПРИЯТИИ
Аннотация
Цель работы — продемонстрировать возможность применения многофакторной регрессии в качестве альтернативы исследованию влияния некоторого профессионального фактора риска на величину стандартизованных показателей специфической заболеваемости, когда фактическая динамика показателей в реальности может быть связана как с профессиональной вредностью, так и со спонтанным развитием изучаемого заболевания с возрастом. Аналоги оценок стандартизованных по возрасту эпидемиологических показателей заболеваемости (ASR, age-adjusted standardized rates) и стандартизованных отношений заболеваемости (SIR, standardized incidence ratios) получены на основе применения гибридного статистического метода. Он сочетает медианные оценки и байесовское моделирование при сохранении принципа стратификации неоднородной выборки на однородные группы в пространстве двух факторов риска, по крайней мере. Для частного случая пропорциональности годовых показателей заболеваемости, когда два фактора действуют независимо (мультипликативное влияние фактора риска на заболеваемость) в рамках пуассоновской статистики событий заболевания строго показана полная эквивалентность методов регрессии и стандартизации.
Использован гибридный статистический метод, объединивший медианное оценивание Коэнкера–Бошковича и байесовские процедуры, в отличие от частотных методов Фишера. Это позволило сосредоточиться на центральной тенденции в анализе редких данных, повысить устойчивость к выбросам, снизить влияние систематических смещений, улучшив соответствие фактической и номинальной вероятности покрытия доверительных интервалов.
Установлено, что метод стандартизации не вполне подходит для эпидемиологического исследования влияния профессиональных рисков на здоровье из-за потери информации при усреднении. Он эффективен только для упрощённого разведочного анализа или оценки обобщенных популяционных санитарных показателей. Однако сочетание медианного оценивания и байесовского моделирования позволяет заменить как стандартизацию, так и множественную пуассоновскую регрессию, сохраняя их достоинства и расширяя возможности исследования при нарушении свойства пропорциональности показателей заболеваемости.
Стандартизацию и даже пуассоновскую регрессию методом максимального правдоподобия следует заменить медианной регрессией байесовских оценок в стратах. В противном случае традиционный подход приводит к недооценке фактических рисков заболевания или к количественному смещению их оценок.
1. Введение
Оценка и учёт профессиональных рисков — обязанность каждого работодателя. Если это касается рисков травматизма или инфекционных заболеваний, связь между причиной и следствием, как правило, сравнительно легко обнаруживается в силу небольшого временного разрыва между событиями. Совсем иначе дело обстоит с потенциальной возможностью приобретения работником хронических (длительно развивающихся или стойких) профессиональных заболеваний, когда связь между действием вредного производственного фактора и постановкой диагноза неочевидна или неизвестна. Более того, такая связь может иметь стохастический характер, когда у двух работников, находящихся в одинаковых производственных условиях, исход за одинаковый период наблюдения может быть совершенно различным. Подобных примеров за 20 и 21 века накоплено огромное количество. В основном, это — результат профессиональных рисков, связанных с причинением вреда здоровью в результате воздействия множества возможных факторов — шума, вибраций, ионизирующего излучения, специфических химических агентов, микроорганизмов, напряжённости трудового процесса.
Очевидно, оценка профессионального риска должна производиться с учётом вероятностного характера событий причинения вреда здоровью (или жизни). Сделать это можно или с помощью инструментов прогнозирования (индивидуального моделирования) в том случае, если физиологические механизмы, связывающие причины и следствия известны; или путем сравнительной оценки вероятностных показателей в двух или более однородных группах работников с учетом наличия и отсутствия фактора риска. Чаще всего на предприятии какие-либо знания о физиологических механизмах взаимодействия факторов риска и его величины отсутствуют. По этой причине фактически единственным инструментом исследования врача-гигиениста являются статистико-эпидемиологические методы, применение которых обычно сопряжено с неоднородностью выборки исследуемых работников. Среди таких методов известна стандартизация популяционных показателей, являющаяся попыткой проведения так называемого «поперечного» исследования. Она достигается путем усреднения показателей по стратифицированным возрастным (продольным) подгруппам выборки, что при некоторых условиях может приводить к потере информации.
Целью предлагаемой статьи является демонстрация иной методики мониторинга динамики групповых интенсивностей заболеваемости или смертности в выделенных когортах сравнительно небольшого размера (до нескольких тысяч человек), исключающей влияние маскирующего усреднения вместе с сохранением принципа стратификации.
2. Методы и принципы исследования
Наиболее часто в качестве дескриптивных вероятностных показателей используется как абсолютные, так и относительные интенсивности изучаемой специфической заболеваемости. Их численные значения, собственно, указывают на состояние здоровья профессиональных групп. Абсолютные показатели известны также как годовая заболеваемость, показатели силы заболеваемости или показатели риска (hazard, incidence). Для вновь возникающих изучаемых хронических заболеваний они обычно измеряются в долях от условно однородной выборки (некоторой страты пространства факторов) за год наблюдений, связанный с возникновением новых случаев специфического заболевания. В силу редкости новых заболеваний, их число за короткие периоды наблюдения является случайной величиной, подчиняющейся распределению Пуассона , :
где m — число возможных новых специфических событий заболевания, ассоциированное с фактическим приращением человеко-лет наблюдения A для однородной страты; h — гипотетическая «истинная» эффективная интенсивность специфических событий, усредненная за период наблюдения. Важно отметить, что это — условная плотность распределения вероятности, для которой непрерывные оценки интенсивности h неизвестны, в то время как дискретное число событий m апостериорно наблюдаемо. Собственно, неизвестные и прямо не наблюдаемые показатели h как раз и подлежат определению при различном сочетании факторов риска. В силу своей природы, такая задача не является легко выполнимой, и обычно оценку h заменяют некоторыми усредненными прямо вычисляемыми статистиками на основе частотного (фишеровского) подхода, в котором вероятностные характеристики подменяются комбинациями фактически наблюдаемых величин. Например, для однородных страт со сравнительно узкими возрастными интервалами наблюдения зачастую вместо h используется точечная оценка
где
Таблица 1 - Структура исходных данных для прямой стандартизации и сравнения показателей
Возрастной интервал (1-й фактор, лет) | Вес w | Интактная группа (2-й фактор Fct = 0) | Группа риска (2-й фактор Fct = 1) | ||
Случаи, m | Число чел.-лет, A | Случаи, m | Число чел.-лет, A | ||
[15 – 20) | 0,1 | 0 | 59940 | 0 | 36634 |
[20 – 25) | 0,1 | 0 | 65701 | 0 | 44278 |
[25 – 30) | 0,1 | 1 | 91382 | 1 | 43878 |
[30 – 35) | 0,1 | 3 | 57408 | 1 | 19672 |
[35 – 40) | 0,1 | 4 | 34178 | 3 | 17876 |
[40 – 45) | 0,1 | 9 | 31200 | 7 | 16222 |
[45 – 50) | 0,1 | 10 | 18526 | 11 | 12736 |
[50 – 55) | 0,1 | 13 | 12824 | 11 | 7236 |
[55 – 60) | 0,085 | 11 | 6356 | 10 | 3864 |
[60 – 65) | 0,065 | 9 | 3027 | 8 | 1848 |
[65 – 70) | 0,05 | 4 | 995 | 9 | 1275 |
Эффективные значения | 1 | 34,2 | 41220 | 46,9 | 36810 |
Примечание: набор весов в различных возрастных интервалах приблизительно соответствует так называемому «европейскому стандарту» распределения работников по возрасту для диапазона от 15 до 70 лет
Описанная процедура оценки стандартизированных показателей и их отношения, несмотря на общеизвестность, обладает рядом очевидных недостатков, приводящих к смещению оценок. Среди них
а) наличие погрешности дискретизации оценок
б) систематическая недооценка точечной величины
в) потеря информации или её ошибочная трактовка в результате процедуры усреднения показателей по всем возрастным интервалам, что противоречит намерению научного исследования связи риска с его причинными факторами. Например, известны ситуации, когда различия в двух популяциях статистически значимы при попарном сравнении страт в одинаковых возрастных группах одновременно с парадоксальным отсутствием статистически значимых отличий по стандартизованным показателям и наоборот;
г) навязывание , , , гипотезы о нормальном распределении стандартизованных показателей при обобщённом исследовании совокупности пуассоновских наблюдений, что приводит как к систематическому смещению оценок, так и к ошибкам в оценке их неопределенности, а также к абсурдному ожиданию конечной вероятности «наблюдения» отрицательных значений для заведомо положительных показателей.
Таким образом, оценка стандартизованных показателей риска имеет смысл не сама по себе, а в качестве определения величин, которые могли бы наблюдаться при определенных условиях. Показатели ASR заимствованы эпидемиологами из арсенала методов санитарной статистики , как средство планирования пропускной способности региональных лечебных учреждений. Однако они не вполне способны корректно описать изменения истинных показателей заболеваемости вследствие влияния неких профессиональных факторов неоднородности выборочных наблюдений. Ввиду резкой возрастной зависимости для большинства изучаемых заболеваний больше смысла имело бы прямое сравнение наблюдаемых показателей по соответствующим возрастным группам. Однако такой приём связан с дроблением выборок на страты и уменьшением числа случаев в сопоставимых стратах, которое приводит к потере статистической значимости различий. Для сохранения или улучшения значимости следует производить сравнение сразу по всей совокупности наблюдений вместе с сохранением принципа попарного сравнения страт во всей неоднородной выборке. Это очевидным образом приводит к использованию идеи регрессии показателей по всем факторам риска. Особо укажем, что речь должна идти о регрессии центральных (по вероятности) значений, что приводит к идее оценки медианных тенденций или трендов.
Подходящим инструментом исследования в этом случае может быть сочетание статистического моделирования со статистическим оцениванием и использованием внутреннего «контроля», аналогично методу максимального правдоподобия Фишера, оперирующего подходящими вероятностными распределениями и моделями детерминированных «зависимостей». Однако, в отличие от метода Фишера, следует отказаться от принципа максимизации правдоподобия измеряемой величины, приводящего к смещению центральных оценок в условиях недостаточной мощности наблюдений, сохранив концепцию использования математической оптимизации как удобного вычислительного приёма. Оказывается, прототип такого метода известен — это медианная (квантильная) регрессия Коэнкера, получившая за последнее время некоторое распространение в статистическом анализе первичных данных, обладающих существенной асимметрией в описании случайного рассеяния , .
Для реализации цели можно связать распределение (1) с сопряженным условным распределением
Относительно характера возможных оценок h, это – известное гамма-распределение, приводящее к корректным центральным вероятностным оценкам
Свойства гамма-распределения диктуют, что ширина 90%-ной области случайной неопределенности непрерывных оценок h для одной страты не превышает центрального значения интенсивности только при числе отсчетов m > 11. Иными словами, показатель при более низком числе отсчётов будет определяться с относительной случайной неопределенностью свыше 50%. Можно видеть также, что при m≤2 в выборке он может вовсе превышать 100%, что лишает всякого смысла получение абсолютных оценок для групп с редкими событиями. Отсюда же понятна необходимость оценки единой модели данных сразу для всей таблицы 1, то есть учёт как можно большего числа «случаев».
Очень наглядно табличные данные могут быть представлены в виде графика с нанесенными точечными медианными оценками интенсивности заболеваемости отдельно по каждой страте. Нетрудно заметить, что хаотичность данных в таблице 1 — лишь кажущаяся. Напротив, на графике отчетливо видны два тренда, соответствующих зависимости от возраста в двух непересекающихся группах, то есть если случайность и присутствует, то её роль в группе наблюдений слабее детерминированного тренда, несмотря на стохастическую природу изучаемого заболевания. Заметная роль мешающего случайного отклонения оказалась характерна только для страт с нулевым или единичным числом случаев. При этом ясно, что при использовании частотных (фишеровских) центральных оценок отклонения от тренда были бы визуально больше изображенных. Иными словами, применение классического принципа максимального правдоподобия для получения точечных оценок к интервальным случайным величинам с асимметричным распределением является источником систематических смещений. В силу этого, в дальнейшем будем придерживаться только байесовского толкования (3).
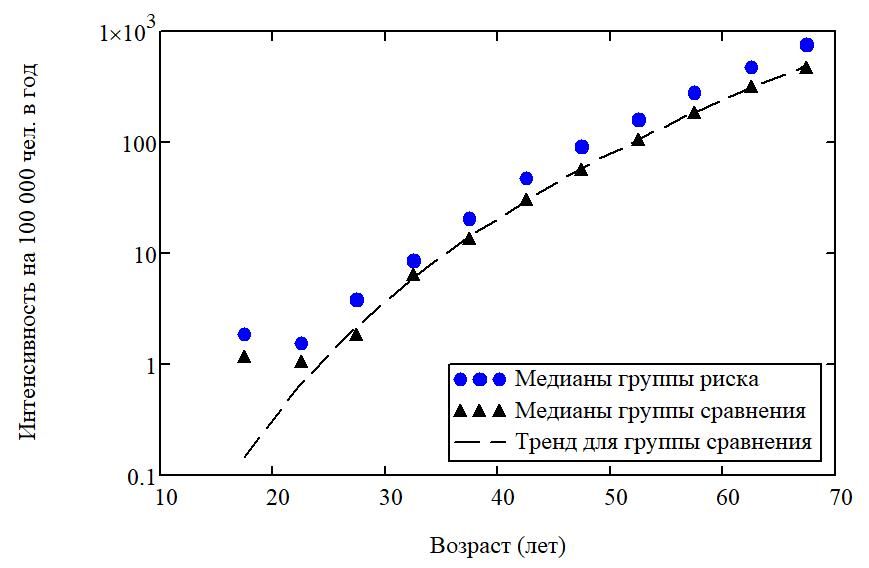
Рисунок 1 - Медианные точечные оценки интенсивности заболеваемости на предприятии для двух подразделений с различной профессиональной нагрузкой
Примечание: 22 страты; на 100 тыс. чел. за год
В рамках такого понимания можно говорить о необходимости выполнения регрессии по модели
Важно ввести понятие минимизируемой нормы аппроксимации медианных точечных оценок, обеспечивших повышение устойчивости наряду с аппроксимационной моделью. Однако оптимизация должна производиться не для пуассоновских вероятностей (1) и не для гамма-распределений (3), а для плотностей распределения вероятностей наблюдения абсолютных отклонений
где ψ(δ) — плотность распределения вероятности модуля отклонения, с возможностью прямой статистической оценки её качества для наилучшей модели. При этом суммирование следует производить по всем стратам табл. 1 с исключением страт, обладающих нулевым числом случаев, как не несущих значимой информации. В этих случаях функционал Ω(β) оказывается непрерывным по компонентам вектора параметров β при mi≥1, но с фактическим ограничением на исследуемый диапазон возрастов от 25 до 70 лет, в котором наблюдения количественно информативны. Минимальное значение Ωmin>0 в случае хорошей аппроксимации можно рассматривать как реализацию случайной величины приблизительно с распределением «хи-квадрат» и с числом степеней свободы df = dim(μ) – dim(β). Критерием хорошего качества аппроксимации будет неравенство Ωmin≤df. Оценку доверительных областей для компонент вектора β в этом случае не следует производить через расчёт информационной матрицы Фишера в силу заметных отклонений распределения оценок параметров модели от нормального (симметричного) закона из-за многократных нарушений симметрии преобразований и исходной асимметрии гамма-распределений (3). Но можно воспользоваться алгоритмом профиля правдоподобия Венцона , невзирая на то, что эта процедура редко применяется исследователями. Численное исследование функционала (4) в приложении к табл. 1 приводит к результату HR=1,58 (90% CI: 1,16-2,15) ; P=0,007 (см. рис. 2). При этом эмпирическое распределение возможных оценок отношения показателей заболеваемости оказалось очень близко к логнормальному профилю, как это теоретически и ожидалось традиционно для относительных исследований , , , .
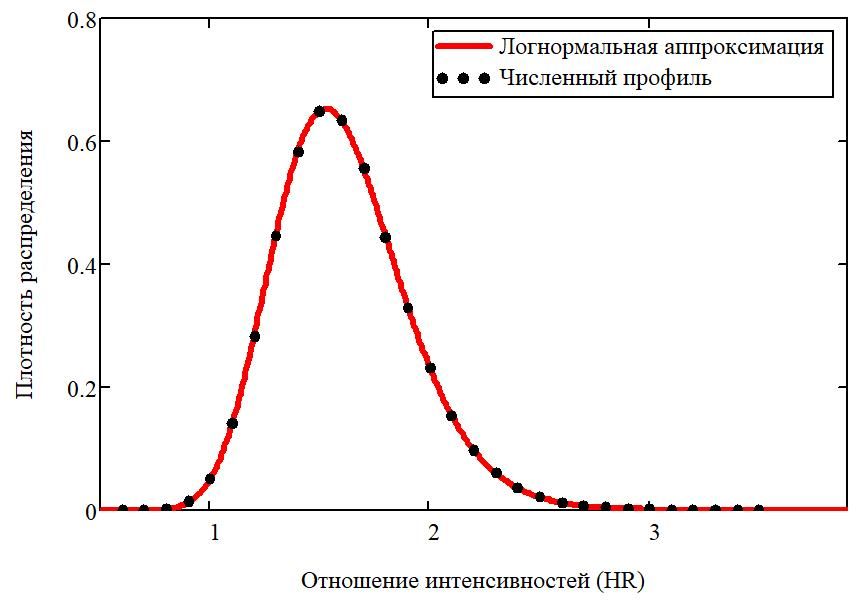
Рисунок 2 - Распределение оценок hazard ratio методом медианной регрессии при сравнении референсной и рисковой групп по всей совокупности ненулевых наблюдений
3. Проверка соответствия показателей HR и SIR для условий соблюдения пропорциональности показателей hazard в рамках байесовского оценивания
Формально, стандартизованный показатель ASR интенсивности заболеваемости задан выражением (2), однако в рамках байесовского оценивания на самом деле следует использовать линейную комбинацию
где hi — непрерывные случайные значения интенсивности во всех изучаемых возрастных интервалах; wi – «стандарт» распределения численности выборки по возрастным интервалам.
Однако непосредственное использование выражения (5) затруднено из-за сложности распределения величины λ. Причина в том, что линейная комбинация (композиция) одиннадцати независимых гамма-распределенных случайных величин является, в общем случае, сложным распределением с 33 параметрами, привязанными к стратам табл. 1. Его плотность вероятности может быть вычислена в интегральной форме с применением преобразования Лапласа, но только не через элементарные функции. Исключением является случай, когда соотношения Ai/wi одинаковы для всех страт i=1...11, а параметры формы mi — натуральные. Тогда λ также подчиняется гамма-распределению (распределению Эрланга) с суммарным натуральным параметром формы. По этой причине в вычислительной практике удобнее использовать аппроксимацию точного распределения. Очевидно, можно опираться на то обстоятельство, что при любых неотрицательных параметрах mi, Ai, wi итоговая плотность распределения вероятности для λ всегда имеет унимодальный профиль с нулевыми асимптотиками на краях области определения, напоминающий гамма-распределение с некоторыми эффективными и не обязательно целочисленными параметрами meff, Aeff. Найти их можно, приравняв точные значения математического ожидания и дисперсии для λ точным их аналогам распределения (3) с эффективными величинами meff, Aeff:
Система (6) всегда имеет единственное решение:
Например, для совокупности наблюдений таблицы 1 эффективные параметры указаны в последней строке таблицы, откуда видно, что оценки стандартизованных показателей заболеваемости ASR имеют весьма отдалённое отношение к так называемым «грубым показателям» заболеваемости и годовой интенсивности заболеваемости. Тем не менее, с несколько иных позиций, но они повторяют так называемую гамма-стандартизацию Фэя и Фейера , которая проверялась Тивари и была признана наиболее точно сохраняющей фактический уровень вероятности покрытия с уровнем, близким к номинальному. Конкретно для данных таблицы 1 по формулам (5–7) можно получить следующие почти не перекрывающиеся оценки: для референсной группы
где 2F1(*) гипергеометрическая функция Гаусса, Γ(*) – полная гамма-функция Эйлера. Для рассмотренных эффективных параметров таблицы 1 это даёт P{λ(1)≤λ(0)}=0,027, что заметно меньше типично принимаемого критического уровня статистической значимости 0,05. Этот факт прямо свидетельствует о незначительности перекрытия доверительных интервалов для стандартизованных среднегодовых показателей ASR в диапазоне возрастов от 15 до 70 лет. По аналогии с методиками оценки показателя SIR как стандартизованного отношения показателей заболеваемости , , , , отношение медиан может рассматриваться в качестве центрального значения SIR≈1,53. Однако его доверительный интервал может быть строго оценен только при условии определения плотности распределения вероятности для отношения двух случайных величин
4. Главное преимущество регрессии в сравнении со стандартизацией
Возможности медианной регрессии, очевидно, должны оказаться более широкими, если предположение о пропорциональности показателей интенсивности заболеваемости не будут соблюдаться. В таких ситуациях методы стандартизации показателей могут привести к существенной недооценке роли фактора риска и даже к ошибочной оценке знака эффекта. В отличие от этого, модельный подход при удачном выборе модели не позволит потерять или исказить ценную информацию. Очевидно, факт SIR≠HR должен уже сам по себе свидетельствовать о нарушении гипотезы о пропорциональности моделей риска. И это не такая уж редкость. Например, при изучении заболеваний раком щитовидной железы в когорте Национального радиационно-эпидемиологического регистра в представительной группе 18+ лет (746 случаев из 211 939 наблюдений) обнаружено SIR = 3,71 (95% ДИ: 3,43 … 4,01) в процессе применения метода стандартизации показателей. Однако для тех же данных в процессе пуассоновского моделирования одновременно наблюдался отрицательный тренд HR по дозе ионизирующей радиации. Такой факт обнаружен в пределах одной публикации, но авторы парадоксальным образом не увидели в этом никакого противоречия… Возможно и наоборот: применение метода стандартизации указывает на наличие статистически значимой отрицательной связи показателей заболеваемости раком печени в условиях профессионального хронического ионизирующего облучения в крупной объединенной когорте атомной промышленности США (101 363 работника; 348 случаев). Однако похожее исследование фиксирует аналогичную положительную восходящую связь между HR и дозой в условиях острого облучения среди выживших после атомной бомбардировки. И где же истина? Очевидно, более правильно здесь было бы говорить о получении смещённых статистических оценок, причём причиной смещения являлся сам алгоритм статистической обработки.
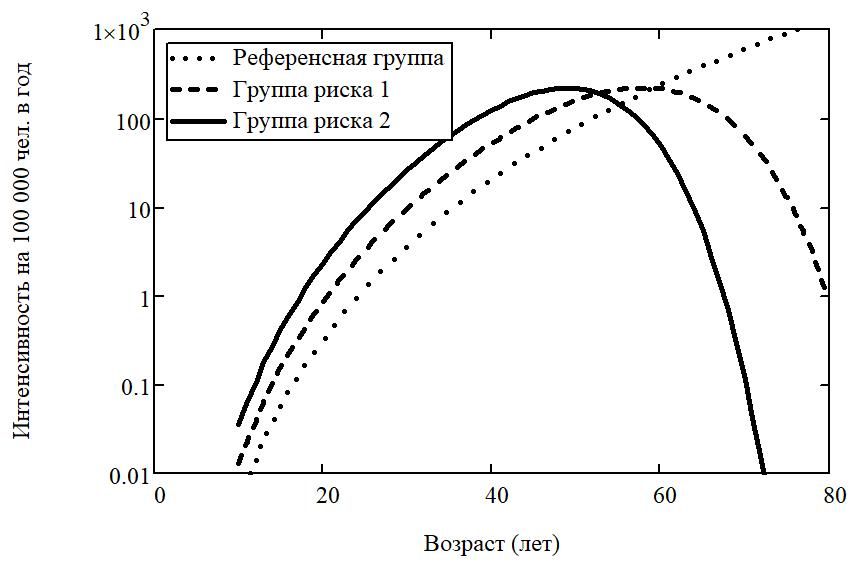
Рисунок 3 - Гипотетические зависимости интенсивности заболеваемости от возраста с одинаковой величиной ASR
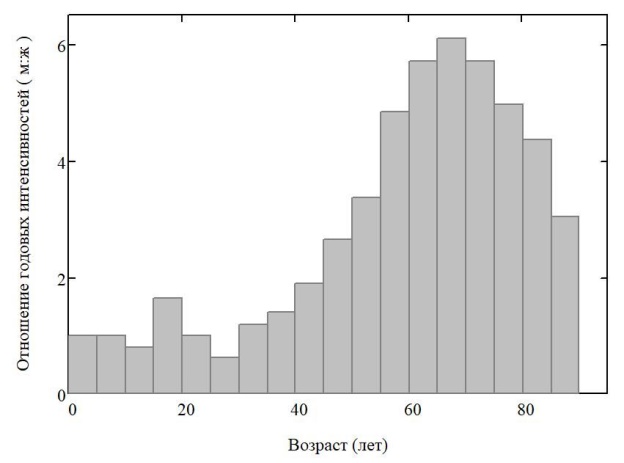
Рисунок 4 - Нарушение пропорциональности интенсивностей групповой заболеваемости для мужчин и женщин при изменении возраста
5. Заключение
Со всей определенностью можно утверждать, что не целесообразно использовать метод стандартизации показателей заболеваемости с целью эпидемиологического изучения влияния факторов профессионального риска на здоровье персонала предприятий как универсальный способ поперечного исследования, т.к. это может приводить к потере информации в процессе статистического усреднения. Вместе с тем, сам принцип стратификации неоднородных наблюдений в пространстве конкурирующих факторов риска (с дальнейшим использованием пуассоновских отсчётов для регрессии) должен быть сохранён. Однако регрессию методом максимального правдоподобия следует заменить медианной регрессией байесовских оценок в стратах, игнорируя страты с нулевым числом случаев, как неинформативные.
Стандартизация показателей интенсивности заболеваемости может быть использована, исключительно, либо для упрощённого разведочного статистического анализа, либо по прямому назначению — в качестве метода оценки усредненного по возрасту показателя для целей санитарной статистики.
